M系列をscipyで生成する

M系列とは、原始多項式によって生成される系列です。原始多項式の次数を$k$とすると、符号長は$L = 2^k -1$となります。また、自己相関は $$ r_{ff}(n) = \cases{ 1 & n = 0 \cr -\frac{1}{L} & \text{otherwise} } $$ と表されます。(M系列に対する詳しい説明はこちらを参照してください。)

以下でscipyを用いたM系列の生成を行っています。

import numpy as np
from scipy.signal import max_len_seq
from numba import jit
import matplotlib.pyplot as plt

def mls(n, taps=None):
	mls_b = max_len_seq(n, state=None, taps=taps)[0] # M系列を生成
	return np.sign(mls_b - 0.5) # {0,1}のビットから{-1,1}のビットに変換

@jit('f8[:](f8[:],f8[:])', nopython=True) # 相関値を見るための関数
def correlate(v1, v2):
	res = []
	for i in range(v1.shape[0]):
		res.append(np.correlate(v1, np.roll(v2, i))[0])
	return np.float64(res)

n = 5 # 原始多項式の最大次数
taps = [3, 2, 1] # 原始多項式で係数が1となる次数を列挙(最大次数と定数項は不要)
m1 = mls(5, taps=taps)
plt.plot(correlate(np.float64(m1), np.float64(m1))/(2**n-1))

この場合、原始多項式$f(x) = x^5 + x^3 + x^2 + x^1 + 1$によるM系列が生成されます。自己相関は以下のようなグラフとなり、正しくM系列が取れていることがわかります。

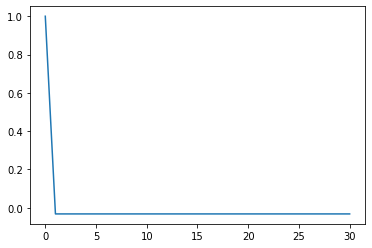
ちなみに、scipy.signal.max_len_seq()のstateパラメータはシフトレジスタの初期設定値が与えられます。省略すると、適当な初期値でM系列が生成されます。

参考