Gold符号をpythonで生成

「M系列をscipyで生成する」にてM系列についての説明をしました。ここでは生成したM系列よりGold符号を生成する方法を説明します。

Gold符号は、符号長$L$のpreferred pairなM系列$a(t),b(t) \in \{1, -1\}^L$を用いて以下の式で表現されます。

\[ Gold(l) = a(t) \otimes b(t+l) \quad 0 \leq l \leq L-1 \\ Gold(L+1) = a(t) \\ Gold(L+2) = b(t) \]

ここで、preferred pairな系列とは相関値が3種類の値のみをもつM系列のペアのことです。具体的には、以下のようなものが挙げられます。（参考）

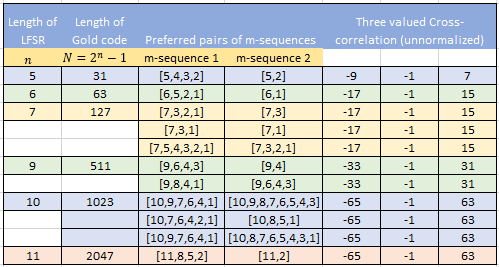
M系列と比較して、相互相関の優れた系列を多く生成することができます。

以下でscipyを用いてM系列の生成を行い、Gold符号を生成します。

import numpy as np
from scipy.signal import max_len_seq
from numba import jit
import matplotlib.pyplot as plt

def mls(n, taps=None):
	mls_b = max_len_seq(n, state=None, taps=taps)[0] # M系列を生成
	return np.sign(mls_b - 0.5) # {0,1}のビットから{-1,1}のビットに変換

@jit('f8[:](f8[:],f8[:])', nopython=True) # 相関値を見るための関数
def correlate(v1, v2):
	res = []
	for i in range(v1.shape[0]):
		res.append(np.correlate(v1, np.roll(v2, i))[0])
	return np.float64(res)

n = 6
m1 = mls(n, taps=[5, 2, 1]) # 原始多項式f1による構成
m2 = mls(n, taps=[1]) # 原始多項式f2による構成
plt.plot(correlate(np.float64(m1), np.float64(m2))/(2**n-1))

原始多項式$f_1(x) = x^6 + x^5 + x^2 + x^1 + 1$と$f_2(x) = x^6 + x^1 + 1$によるM系列は、相互相関値が以下のグラフのように3種類のみとなっており、preferred pairの関係にあります。

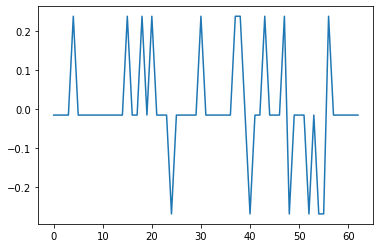
この系列を用いて適当な2種類のgold符号を生成してみます。

gm1 = m1 * np.roll(m2, 1)
gm2 = m1 * np.roll(m2, 2)
plt.plot(correlate(np.float64(gm1), np.float64(gm1))/(2**n-1))
plt.plot(correlate(np.float64(gm1), np.float64(gm2))/(2**n-1))

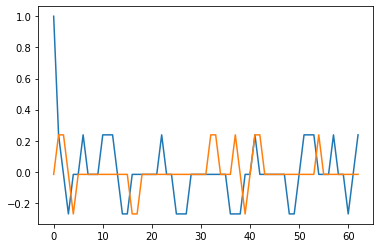
以下のグラフがgold符号の自己相関と相互相関を表します。青がgm1の自己相関、オレンジがgm1とgm2の相互相関です。両者ともによい相関を持っていることが確認できます。